Optica experimenten met Luctor's Experimenteerset en CoachLab

Datum: Juni - December 2025

Inleiding:

Recentelijk kon ik deze zeer mooie experimenteerset bemachtigd. Op de handleiding na compleet. Gelukkig heb ik de handleiding al eens eerder kunnen scannen.

Principe:

Experimenteren met lichtstralen, spiegels en lenzen.

Materiaal:

  • Luctor's Optica Experimenteerset
  • Computer met Excel en CoachLab software geïnstalleerd
  • CoachLab II
  • CMA Lichtsensor (0513)
  • Luxmeter
  • Milimeterpapier (Grafiekpapier)
  • Knijper
  • Passer
  • Potloden


 

 

Uitvoering, resultaten, discussie en conclusies:

Experiment 1: licht plant zich rechtlijnig voort

Plaats de lamp op 0, een houder met een horizontale spleet op 20 en het scherm op 35. Roteer het scherm dusdanig dat het bijna gelijk georiënteerd is met de geleider.

Men kan een rechte lichtbundel waarnemen op het scherm. Licht beweegt zich dus rechtlijnig voort. Een lijn, waarlangs het licht zich voortplant noemt men een lichtstraal.

Experiment 2: Schaduwen

Plaats de lamp op 0, het scherm op 55 en bevestig een potlood of pen in een houder geplaatst op 35 cm.

Men kan een scherp afgetekende donkere figuur van dezelfde vorm als de pen op het scherm waarnemen. Aangezien licht zich rechtlijnig voortplant  wordt het niet doorgelaten door een ondoorzichtig voorwerp en tekent zich een schaduw af achter het voorwerp.

Bevestig nu een houder op 7 en plaats daar een witte matglasplaat in. Het glas wordt verlicht en treedt nu als lichtbron op.

We hebben nu een scherp lichtbron (gloeidraad, klein oppervak) vervangen door een meer diffuse lichtbron (groot oppervlak). De scherpe schaduw is nu verdwenen, we kunnen zones waarnemen, in het midden een diepe schaduw, aan de randen een half-schaduw.
 

Experiment 3: Verlichting en lichtsterkte

Plaats de lamp op 0 van de schaal. Zorg ervoor dat de gloeidraad van de lamp gelijk is aan de uitgang van de buis (positie 6). Bevestig het frame met het plaatje met een vierkante opening (2x2 cm) op 16. Plaats het beeldscherm in een houder op bv 40. Gebruik mm papier i.pv. een wit vel.
   

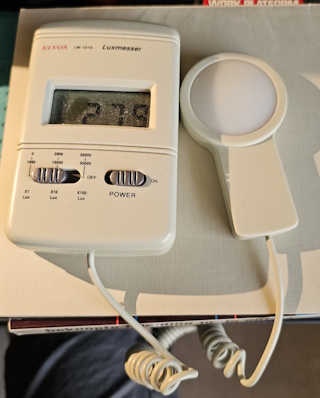
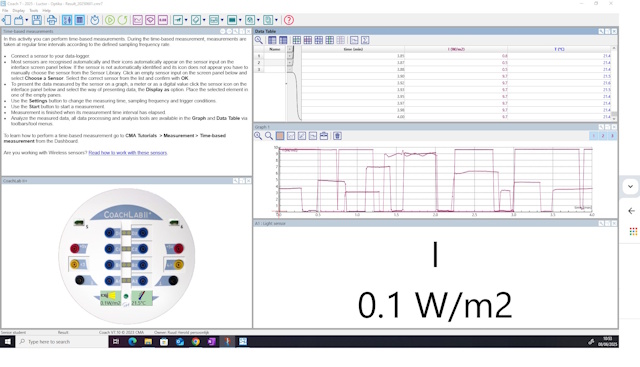
Varieer de afstand tussen scherm en frame (25, 30, 35, 40, 45, 50 cm) en meet steeds de dimensies van de projectie op het scherm.

Herhaal dit experiment met de belichtingsmeter bevestigd in het midden van de projectie zoals weergegeven in nevenstaande foto.

Herhaal dit experiment ook met de lichtintensiteitsmeter van CoachLab. Bouw de opstelling op zoals weergegeven in onderstaande foto. Gebruik een frame met een plaatje met een rondje om de lichtmeter in te plaatsen i.p.v. het scherm. Plaats de lichtmeter ook op een steun zodat deze horizontaal blijft. Exporteer de resultaten als CSV file en importeer deze in Excel voor verdere analyse.

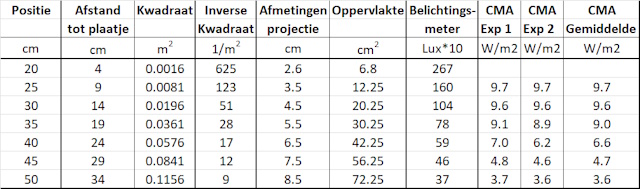
De resultaten zijn samengevat in onderstaande tabel:

De projectie van het vierkant wordt groter naarmate de afstand toeneemt. Visueel kunnen we ook waarnemen dat de projectie donkerder wordt, de verlichting wordt dan minder.

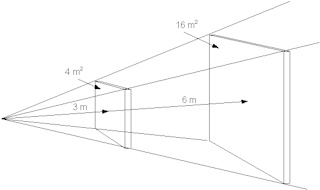
    Als we nu aannemen dat het licht zich gelijkmatig verspreid in alle richtingen en vanuit een puntbron komt dan kunnen we nevenstaande schets maken. We beschouwen slechts een deel van het licht dat uit de puntbron vertrekt. Naarmate de afstand tot de bron groter wordt verspreid het licht zich over een groter oppervlak en lijkt het alsof de intensiteit afneemt. Dit suggereert dat de intensiteit van het licht omgekeerd evenredig is met het oppervlak waar het op valt.
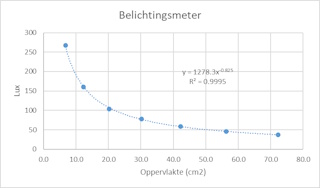
In formule: I α 1/A
Elk van de vierkanten in de schets is evenredig met de afstand van de puntbron. Dit betekent dat het oppervlak van elk vierkant recht evenredig is met het kwadraat van de afstand (d).
In formule: A α d2
Gecombineerd: I α 1/d2

Deze formule zegt dat de lichtintensiteit afneemt met het kwadraat van de afstand. Deze formule kunnen we dan weer controleren met onze lichtintensiteitsmetingen. Kijken we eerst naar de belichtingsmeter metingen.
   
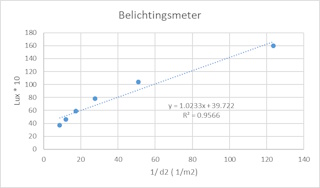
De linkergrafiek laat de respons van de lichtmeter als functie van het projectieoppervlak zien. De grafiek laat duidelijk zien dat de response afneemt als de afstand toeneemt. De grafiek laat ook zien dat response groot is als de meter dicht bij de lichtbron is (alle licht valt op de sensor) maar de verschillen duidelijk kleiner worden als de afstand "groot" is (oppervlakte projectie groter dan de sensor). Dat zijn twee locaties waar de meting onnauwkeuriger wordt hetgeen we ook kunnen zien in de rechtergrafiek waar we de formule uitgezet hebben. 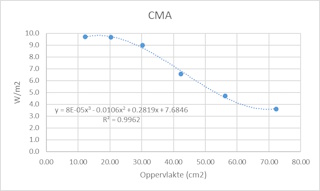We zien nog steeds een lineaire relatie maar de uitersten trekken de rechte krom.
Soortgelijke problemen kunnen we waarnemen bij de Coachlab metingen.
   
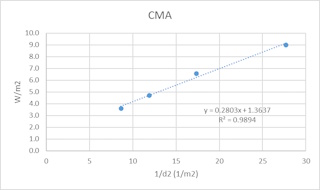
Het meetbereik van de sensor is 0,1 W/m2 tot 10 W/m2. Waardes boven de 9 W/m2 zijn niet meer representatief. Laten we deze buiten beschouwing dan kunnen we inderdaad een duidelijk lineaire relatie waarnemen. Dit experiment laat ook goed zien dat we bij metingen de karakteristieken van de meetsensoren in beschouwing moeten nemen.
 
Experiment 4: Vlakke spiegel
Duw de lamp zo ver mogelijk terug in de buis. Bevestig de lens (+10 cm) op 13,  een frame met een schild met horizontale spleet op 16 en het beeldscherm op 30. Draai dat laatste zo dat er een scherpe lichtstraal op het papieroppervlak valt. Bevestig de vlakke spiegel met schaal op het scherm dusdanig dat er een rechte lijn op 0 verschijnt, zoals weergegeven in onderstaande foto. Lees de hoek af tussen de normaal en de invallende straal (hoek van inval) en vergelijk dit met de hoek tussen de normaal en de teruggekaatste straal (hoek van terugkaatsing). Draai de spiegel zo dat ander hoeken worden verkregen.
De resultaten zijn weergegeven in onderstaande foto's:
   
    10 ° 40 °
   
    30 ° 20 °
Lezen we de hoek af tussen de normaal en de invallende lichtstraal (hoek van inval) en deze vergelijken met de hoek tussen de normaal en teruggekaatste straal (hoek van terugkaatsing) dan observeren we dat de hoek van inval altijd gelijk is aan de hoek van terugkaatsing (reflectiehoek).
Vervang het plaatje met maar een spleet door een plaatje met 5 spleten
De vijf evenwijdige stralen die op de vlakke spiegel vallen worden parallel van elkaar gereflecteerd.
Beweeg de lens dichter naar de lichtbron zodat de lichtstalen zich verspreiden (divergeren).
Divergerende stralen die op een vlakke spiegel vallen blijven ook na reflectie divergerend.
   
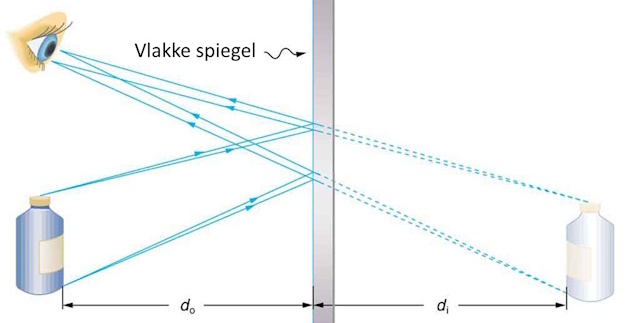
Verwijder alle onderdelen op een framehouder na. Bevestig de vlakke spiegel in het frame en plaats deze op 20 met de reflecterende kant naar de veren gedraaid.

Schroef een potlood in een houder op bv 5 en observeer, Het beeld van het potlood in de spiegel schijnt zich achter de spiegel te vinden.

Bevestig een ander potlood in een houder echter de spiegel. Beweeg het potlood voor- en achteruit en observeer tegelijkertijd het spiegelbeeld van het potlood voor de spiegel.

Op een bepaald punt van de schaal lijkt het bewegende potlood een voortzetting van de andere te zijn. Het potlood staat dan op dezelfde plaats staan als het spiegelbeeld van het potlood van voor de spiegel. De afstand tot de spiegel is dezelfde als de afstand  van het potlood voor de spiegel tot de spiegel.

Het spiegelbeeld van een voorwerp ligt altijd evenver achter de spiegel als het voorwerp zelf ervoor ligt.
Rechts en links zijn echter omgedraaid, zoals weergegeven in onderstaande schets.
 
Experiment 5: Gebogen spiegels
Plaats de lamp op 0, bevestig de lens (+10) op 13 (vlakke deel richting lamp) en het frame met het schild met de 5 horizontale strepen op 16. Het beeldscherm wordt op 30 geplaatst en zo gedraaid dat het bijna evenredig is aan de schaal. Bevestig de holle spiegel met de klemveer op het scherm. Beweeg de lamp voor- of achterwaarts in de buis zodat de lichtstralen evenwijdig worden. Draai het scherm zo dat het licht zo helder mogelijk wordt.
    De parallel lopende invallende lichtstralen gaan na terugkaatsing , door een punt, het brandpunt van de holle spiegel.

Markeer m.b.v. een potlood het brandpunt en de gebogen vorm van de spiegel.

Verwijder het grafiekpapier en gebruik een passer om de  brandpuntsafstand en de straal van de spiegel te bepalen.

De brandpuntsafstand is gelijk aan de halve straal van de spiegel.
Met dezelfde opstelling draaien we de holle spiegel om zodat deze een bolle spiegel wordt. De lichtstralen divergeren nu waarbij het lijkt alsof hun oorsprongspunt (brandpunt) achter de spiegel ligt.
Teken de plaats van dit punt aan m.b.v. potlood en liniaal. Dat dit niet zo gemakkelijk is kan men aan onderstaande foto zien. Door de divergentie is de lijn van de straal niet altijd duidelijk in te tekenen.
In de handleiding beschrijft men nu een experiment om de lichtbundels zichtbaar te maken met behulp van tabaksrook of kalkstof. Ik rook al jaren niet meer en om kalkstof rond te spuiten in mijn studeerkamer gaat met iets te ver. Ik heb een poging gedaan met waterdamp door een kleine donut humidifier in een bakje water te leggen en dat werkt een klein beetje, voor een klein deel van de bundel. Ik heb overwogen om een vapepen te kopen en die te gebruiken om wat meer mist te maken maar ook dat ging me iets te ver. Onderstaande foto komt uit de handleiding en laat zien wat de bedoeling was. 
De lichtstralen komen komen na reflectie samen op een bepaald punt (brandpunt) en divergeren daarna weer.
Verwijder de lens van de bank en plaats een frame op 7 cm voor de lamp. Plaats een L L-vormige spleet in het frame samen met een witte matgas plaat. Plaats de hol/bolle spiegel (concaaf/convex) met de holle (concave) zijde naar de lamp. Draai de spiegel zo dat deze enigszins scheef staat t.o.v. de bank. Probeer de teruggekaatste lichtstralen op een scherm te projecteren.
Er verschijnt een L-vormig (ietwat verwrongen) beeld verschijnen op het scherm waarbij de L omgekeerd is (omgedraaid en zijdelings gedraaid).  Dit noemt men een reëel beeld. Onderstaande schets geeft weer hoe dit beeld tot stand komt.

    Bewegen we de spiegel dichter bij de lamp (bv op 40 cm) dan zullen we het scherm verder weg moeten plaatsen om een scherp beeld te krijgen, dat dan echter ook groter is.

Indien men de afstand verkleint tot een die kleiner is dan de brandpuntsafstand kan men geen beeld meer op het scherm verkrijgen.

 
Als men dan in de spiegel kijkt kan men wel een beeld van de L zien. Dit beeld noemt men een virtueel beeld omdat het niet op een scherm kan worden weergegeven.  Het beeld is groter en niet meer omgekeerd.

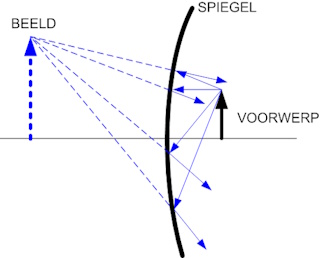
Een holle spiegel produceert altijd, achter de spiegel gelegen, virtuele beelden waarbij het beeld altijd kleiner is dan het voorwerp. In onderstaande afbeelding is schematisch weergegeven hoe dit virtuele beeld tot stand komt.
   
Experiment 6: Breking van het licht
Lichtbreking op het grensvlak tussen twee doorschijnende stoffen
Plaats de lamp op 39 en een +10 lens op 49. Bevestig een frame met een schild met een horizontale spleet op 52. Zet een glazen pot voor 2/3de gevuld met water op een verhoging. Plaat een melkglasplaat achter het vat met water. Houd een vlakke spiegel zo dat een lichtstraal in het vat draait. Probeer dit met verschillende hoeken.
    Als men goed kijkt kan men zien dat de lichtstraal van richting veranderd zodra het wateroppervlak gepasseerd wordt.

Een lichtstraal wordt afgebogen bij het overschrijden van het grensvlak tussen twee verschillende transparante stoffen (hier zijn dat lucht en water).

Zo goed zichtbaar vond ik het effect niet daarom heb ik het experiment herhaald met een groene laserpointer. De breking van het licht is dan duidelijker zichtbaar.
   

Plaats de damp op 0, de +10 lens op 12, een frame met een horizontale spleet op 16 en een scherm op 30 cm. Bevestig een halfronde plexiglasplaat met de klemveer zo, dat de lichtstraal loodrecht op het middelpunt van de rechterzijde valt.  Men ziet dat de straal ongebroken doorgaat.
Een meer theoretische benadering is weergegeven in onderstaande figuur, verkregen door het vertalen van een Commodore 64 Simon's Basic programma naar Lazarus Pascal. Blauwe lichtstralen vertrekken vanuit een lichtpunt (linksonder). Onder een bepaalde hoek treedt totale reflectie op.
    Draai daarna het plexiglas zo dat de straal scheef op de normaal valt.

De invallende straal wordt verdeeld in een weerkaatste en gebroken straal. Voor iedere invalshoek i is er een brekingshoek b die altijd kleiner is dan de hoek van inval. Asl het licht overgaat van een optisch minder dichte in een optisch dichtere stof wordt de lichtstraal gebroken naar de loodlijn toe.

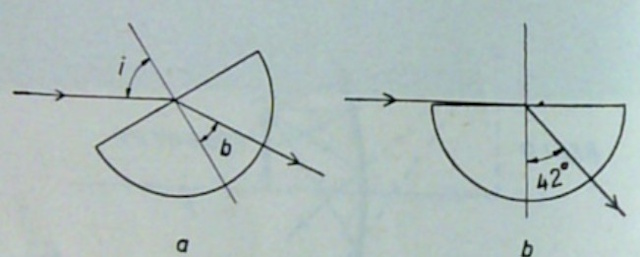
De grootst mogelijke invalshoek is die van 90°. Voor glas komt dit overeen met een brekingshoek van 42°. Voor water is de grenshoek 48°.
    Draai de plexiglasplaat zo dat de straal op de halfronde rand valt. Varieer de hoek waaronder de straal valt. De invallende straal wordt gesplitst in een gebroken en een gereflecteerde straal (r).
   

De lichtstraal gaat van een dichtere (plexiglas )naar een minder dichtere optische stof (lucht). De brekingshoek is groter dan de invalshoek. De straal wordt van de loodlijn afgebroken. Bij een invalshoek van 42° is de brekingshoek 90°.
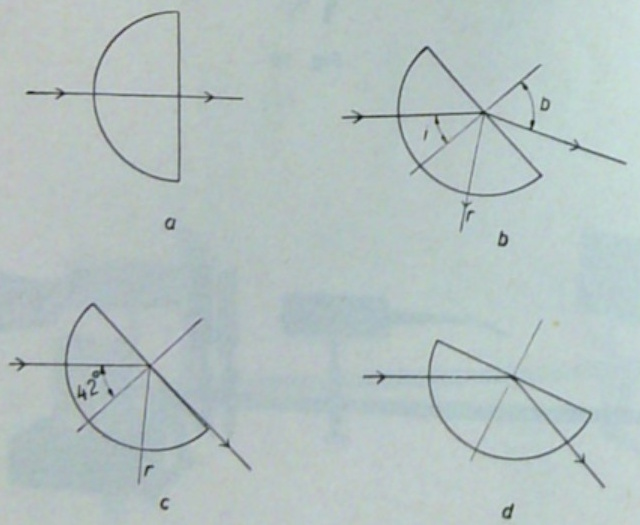    Vervang het beeldscherm voor een bak voor 2/3de gevuld met water. De bedoeling was nu om het van de bak gereflecteerde licht m.b.v een spiegel weer te laten reflecteren op het wateroppervlak.

Dit was echter heel slecht te zien dus besloot ik dit experiment uit te voeren met een laserpointer en zoals men kan zien vindt er totale weerkaatsing van licht plaats op de overgang van water naar lucht.
Straalbreking van een plakke glasplaat
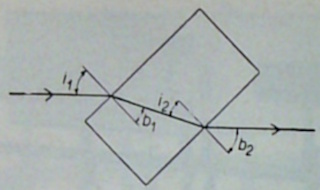
Bouw de vorige opstelling weer op en plaats een rechthoekige plexiglasplaat op het scherm. Draai deze zo, dat de invallende straal verschillende hoeken vormt met de loodlijn op een van de lange zijden van de plaat.
   

De uitgaande straal is altijd evenwijdig aan de invallende maar wordt zijdelings verplaatst. De hoeken b1 en i2 en ook i1 en b2 zijn gelijk (de loodlijnen zijn evenwijdig). De invallende stralen zijn evenwijdig.
   

Indien een lichtstraal door een glasplaat valt, verandert deze niet van richting maar wordt zijdelings verplaatst. De mate van verplaatsing hangt af van de invalshoek en van de dikte van de plaat.
Straalbreking van een prisma
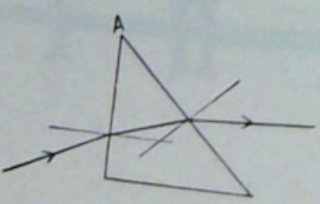
Vervang de plaat door een prisma (met een hoek van 90 ° en twee van 45°). Voer experiment uit met 1 lichtstraal en met 2 lichtstralen. Bedek bij het experiment met twee lichtstralen de onderste spleet met een rood glas.
De invalsstraal wordt eerst gebroken naar de loodlijn toe, gaat door het prisma en wordt bij het uittreden van de loodlijn afgebroken. De hoek A wordt de brekingshoek van het prisma genoemd.
   

   
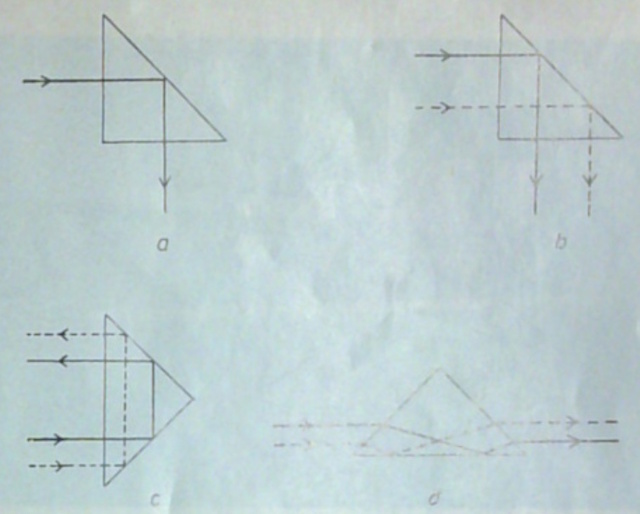
Als een lichtstraal loodrecht op een van de zijden valt bereikt deze de hypotenusa ongebroken onder een hoek van 45°. Deze hoek is groter dan de grenshoek en wordt daarom volledig gereflecteerd. De straal komt er met een rechte hoek aan de andere kant uit.
Bij het experiment met de twee stralen kan men zien dat deze totaal gereflecteerd worden. Bij het gedraaide prisma kan men zien dat de rode straal het prisma onderaan raakt maar bovenaan het prisma verlaat. Ook hier vindt een verwisseling plaats. Een rechthoekig prisma kan gebruikt worden om een beeld om te keren.
 
Experiment 7: Breking van de lenzen
Brandpunt en brandpuntsafstand
Er zijn twee typen lenzen.
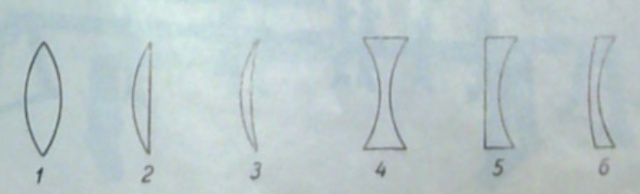  • De covergerende of convexe lens (+ lens) die dik is in het midden en dun aan de uiteinden.
  • De divergerende of concave lens (- lens) die dun is in het midden en dik aan de uiteinden
1. bivonvex  2. planconvex  3. concaaf-convex  4. biconcaaf  5. planconcaaf  6. convex-concaaf
Plaats de lamp op 0, de +10 lens op 13 (met de vlakke zijde naar de lamp), een frame met een 5 horizontale spleten op 16 en een scherm op 30 cm. Bevestig een biconvexe lens  met de klemveer zo, dat de lichtstraal die door het centrum van de lens gaat rechtdoor loopt zonder gebroken te worden. De andere stralen convergeren naar een punt, het brandpunt. De afstand tussen de lens en het brandpunt (F) noemen we de brandpuntsafstand.
Vervang de biconvexe lens door een biconcave lens. De evenwijdige stralen divergeren na de lens gepasseerd te zijn.Het lijkt alsof ze komen vanaf een punt dat voor de lens ligt, het  brandpunt  (F).
Beeldvorming door middel van lenzen
Plaats de lamp op 0, de +15 lens op 15 (met de vlakke zijde naar de lamp), en het frame op 18. Zet het schil met afbeelding (de twee witte punten beneden) in het frame. Zet de +10 lens op 55.  Probeer met het beeldscherm het geprojecteerde beeld opp te vangen.
Het beeld dat gevormd wordt is reëel, verkleind en omgekeerd. Het voorwerp  lgt op een afstand van de lens, die groter is dan de de dubbele brandpuntsafstand.
    Voorwerp
 Beeld
B Het beeld is in werkelijkheid duidelijker maar slecht te fotograferen.
Beweeg de +10 lens naar 38. Het beeld is nu verder verwijderd van de lens.
    Het scherm staat nu op een afstand van ca. 20 cm van de lens. De lens staat op ca. 20 cm afstand van het voorwerp. Het beeld is nog omgekeerd maar van dezelfde grootte als het voorwerp.

Indien de lens op de dubbele brandpuntsafstand van een voorwerp ligt, ligt het beeld op dezelfde afstand van de lens. Het beeld is omgekeerd en even groot als het voorwerp.
   
Verplaats de lens naar 30. Het beeld is nu ver verwijderd van de lens.
    De afstand tussen voorwerp en lens is nu kleiner dan de dubbele brandpuntsafstand. Het beeld is omgekeerd en vergroot.

Indien een lens op een grotere afstand van een voorwerp ligt dan de brandpuntsafstand maar minder dan de dubbele brandpuntsafstand, wordt een vergroot omgekeerd beeld verkregen.
Verplaats de lens naar 24. De afstand tussen lens en voorwerp is nu kleiner dan de dubbele brandpuntsafstand.
    Ongeacht de afstand waar men het scherm plaatst kan men geen scherp beeld meer verkrijgen.

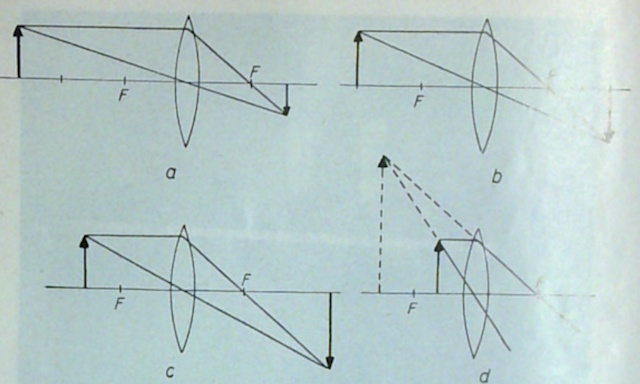
Er verschijnt een rechtopstaand en vergroot virtueel beeld aan dezelfde zijde van de lens als het voorwerp hetgeen men kan zien als men door de lens kijkt.

In onderstaande afbeelding is de beeldvorming van de experimenten schematisch weergegeven (a, b, c, d).
Vervang de + 10 lens door een concave -15 lens.
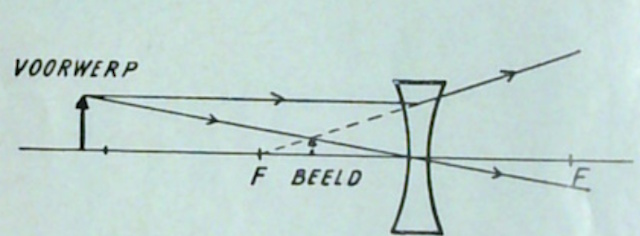
    Ongeacht waar men de lens of het scherm plaatst, het lukt niet om een goed beeld te verkrijgen.

Een convexe lens kan alleen virtuele beelden produceren.

De beeldvorming is schematisch weergegeven in onderstaande figuur.
Gebreken van de beeldvorming door lenzen
Plaats de lamp op 0, een frame met rode glasplaat op 7, het beeldscherm op 55 en de +10 lens op 16 (met de vlakke zijde naar de lamp). Stel de lamp in de hul zo in dat een beeld van de kooldraad op het scherm wordt verkregen. Het is lastig een scherp beeld te krijgen.
    Dit komt doordat de stralen door de buitenranden van de lens niet op hetzelfde punt convergeren als degene die door het middelpunt van de lens gaan.

Hang nu het schild met een ronde opening over de lens. Het beeld wordt scherper doordat allen de stralen die door het middelpunt van de lens gaan het beeldscherm bereiken.

Vervang het schild met een diafragmaschild en we zien dat het beeld minder scherp wordt. Alleen de stralen aan de buitenranden passeren de lens We moeten de lens zelfs een halve cm naar de lamp verschuiven om een redelijk beeld te verkrijgen.

   

Rond

Diafragma
Als het beeld van een voorwerp zuiver door een lens moet worden weergegeven dient de lens te worden voorzien van een diafragma dat alle stralen uitsluit behalve die, die door het middelpunt van de lens gaan.

De geobserveerde afwijking komt in alle eenvoudige lenzen voor en wordt de bolvormige afwijking of sferische alteratie genoemd. Door combineren van verschillende lenzen kan deze afwijking enigermate worden opgeheven.

Ook licht, dat uit verschillende kleuren bestaat , convergeert niet in een punt. De brandpuntsafstand is voor rood licht iets groter dan voor blauw licht. Door een combinatie van convex en concave lenzen van verschillende glassoorten, kan deze kleurafwijking hersteld worden. Zulke lenscombinaties worden achromatisch genoemd.

Verwijder het diafragma van de lens. Draai de lens zo dat het licht schuin op de lens valt. De kooldraad wordt nu afgebeeld als een streep. Alleen als licht in een rechte hoek op de lens valt vormen puntvormige voorwerpen puntvormige beelden. Plaats het beeldscherm dichter bij de lamp. Bij een bepaalde afstand veranderd de horizontale streep in een vertikale.
   
 
Deze lensafwijking wordt astigmatisme genoemd. Indien men een foto van een groep mensen maakt wil men ook dat de mensen aan de randen scherp op de foto staan. Ook deze afwijking kan men wegwerken door een lenzencombinatie.

Er bestaan nog meer lensafwijkingen maar de twee  besproken zijn de meest voorkomende.

 
De camera
In de meest eenvoudige vorm bestaat een camera uit een lichtdichte doos met in de wand een opening met een lens. Aan de zijde tegenover de lens plaatst men dan lichtgevoelige film of, in moderne camera's, een lichtgevoelige sensor.

Een eenvoudig model van een camera maken we door een frame met een matte glasplaat op 0- te plaatsen en de+5 lens op 5 . Daarachter hebben we een voorwerp gezet.  We gebruiken een lamp om het voorwerp goed te belichten (van achteren). Probeer een ze scherp mogelijk beeld te verkrijgen.

   
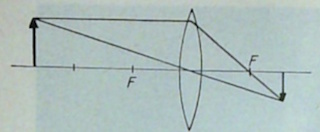
    We verkrijgen een beeld op het matglas dat omgekeerd (de vinger zit onderaan op de standaard) en verkleind is.

De stralengang is weergegeven in nevenstaand schema.
De lens in een camera wordt objectief genoemd.  In moderne camera's is het objectief opgebouwd uit meerdere lenzen, die "samenwerken" om de eerder benoemde lensafwijkingen te corrigeren.

Een ander belangrijk onderdeel van de camera is het diafragma, Het diafragma bepaalt de diameter van de lichtbundel die de lens passeert. Des te kleiner de diafragma opening, des te groter is het vlak waarbinnen het objectief een scherp beeld geeft.

We demonstreren dit effect door in plaats van een lens een schild met een opening van 1 mm te gebruiken. Als voorwerp gebruiken we een theelichtje. We zetten dit alles ook wat dichter op elkaar.
   
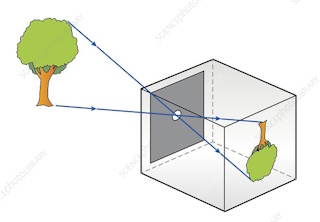
    We verkrijgen wederom een beeld op het matglas dat omgekeerd (de vinger zit onderaan op de standaard) en verkleind is.

De stralengang is weergegeven in nevenstaand schema.
Een algemene opmerking die ik over deze experimenten wil maken is dat het erg lastig was om een herkenbaar beeld te verkrijgen, laat staan een scherp beeld. Typisch een geval waarvan je weet wat je theoretisch kunt verwachten maar het realiseren in de praktijk flink tegenvalt.
 
Het oog
Het oog kan met een fototoestel worden vergeleken. De lens van het oog produceert omgekeerde en verkleinde beelden van voorwerpen op het netvlies. Dat beeld wordt dan door de hersenen geïnterpreteerd. In het oog kan de afstand tussen netvlies en lens niet worden gewijzigd. De juiste instelling wordt verkregen door het brandpunt van de lens te veranderen. De lens is elastisch en omgeven door een ringvormige spier, die het oppervlak van de lens meer of minder sterk kan doen krommen en de brandpuntsafstand veranderen. Het diafragma van het oog is de pupil, die groter of kleiner kan worden waardoor de scherpte van het beeld op het netvlies constant kan worden gehouden.

Een model van een normaal oog dat naar de verte kijkt maken we door een frame met een matte glasplaat op 0 te plaatsen en de +10 lens op 10 . Daarachter hebben we een voorwerp gezet.  Probeer een zo scherp mogelijk beeld te verkrijgen door de lens te bewegen (Fig. a in onderstaand stralengang schetsen)

 

Bij bijziende personen is de afstand tussen lens en netvlies zo groot, dat het de lens niet mogelijk is een scherp beeld op het netvlies te vormen.

Het beeld ligt voor het netvlies binnen het oog (Fig. b).

Vervang de +10 lens door een +5 lens en plaats deze op 9 cm.  Richt het systeem weer op een voorwerp op afstand geplaatst.

Een scherp (omgekeerd) beeld
Een wazig beeld, zonder scherpte.
Om het beeld achterwaarts te plaatsen moet een -15 cm lens voor de +5 cm lens op 12 worden geplaatst. Het kan zijn dat het matgas iets verplaatst moet worden. Door middel van een geschikte concave lens voor het oog kan bijziendheid gecorrigeerd worden (Fig. c).
 
Bij verziende personen is het oog te kort, zodat het door de lens gevormde beeld achter het netvlies komt te liggen (Fig. d). Verwijderen we de concave lens en vervangen we de +5 cm lens door een +15 cm lens op 10 cm geplaatst.
Om het beeld naar voren te halen moet een lens van +30 cm op 15 worden geplaatst. (Fig.e). Door middel van een geschikte convexe lens voor het oog kan verziendheid gecorrigeerd worden.
   
Experiment 7: Projectieapparaten
Diascoop (diaprojector)

 

Bevestig de lamp op 0 en het frame op 13. Zet de dia in het frame met de twee witte punten naar beneden en naar de lamp gericht. Plaats de +15 lens op 32 en beweeg deze zo dat een scherp beeld verkregen wordt op de muur (bij voorkeur 2-3 m).

Bij mij is dat echter een schuin dak hetgeen mij dit besluiten om te projecteren op een dichterbij geplaatst vel papier.
Het beeld is relatief zwak en volledig belicht. Het licht uit de lamp wordt in alle richtingen verspreid en slechts een klein deel daarvan gaat door de dia. Dat deel dat door de dia gaat spreidt ook uit waardoor het uiteindelijke beeld nog zwakker wordt.

Om dat effect tegen te gaan gebruikt men zgn condenserende lenzen, lenzen die het licht concentreren.

Verschuif het frame naar 18 en plaats de +10 cm lens op 15.. Duw de lamp zoveel mogelijk terug in de hals. Plaats de +15 lens op ca. 38 cm en stel zo in dat er een scherp beeld verkregen wordt.

Het gehele beeld wordt nu gevormd en de belichting is regelmatig en sterker.

 Projectie op muur met condenserend lenzen
Projectie op vel papier:
Voor condenserende lenzen
 Na condenserende lenzen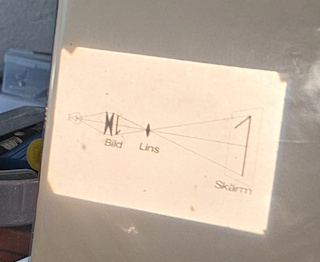
We kunnen het beeld nog scherper krijgen door nog een lens toe te voegen. Plaat de + 5 lens op 7 cm, de + 10 lens op 10 cm en het frame op 13 cm. Zet de + 15 lens op 29 maar verplaats deze zo dat een scherp beeld wordt verkregen. Schuif de lamp verder in de buis om een volledig beeld te krijgen.
   
Episcoop  
Door middel van een episcoop kunnen beelden worden verkregen van ondoorschijnende voorwerpen bv een foto in een boek

We gebruiken hiervoor dezelfde opstelling als in ons laatste experiment maar plaatsen het zo dat het een hoek van 45° met de straal vormt. Teken een figuur op papier en plaats dit in het frame. Het licht van de lamp wordt geconcentreerd door de condenserende lenzen en gericht op de figuur, die sterk belicht wordt.  Het beeld werkt nu als een zelflichtgevend voorwerp en kan gereproduceerd worden, indien een + 15 lens op een geschikte afstand wordt. Het beeld kan zeer goed over een afstand van enkele meters worden geprojecteerd.

De stralengang is weergegeven in nevenstaande schets.

 

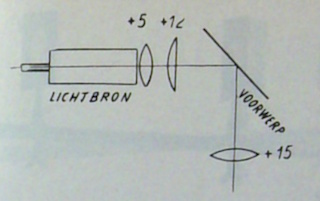
Op de foto kan men een omgekeerd beeld zien.
   
Experiment 8: Enige optische instrumenten

Vergrootglas of loupe
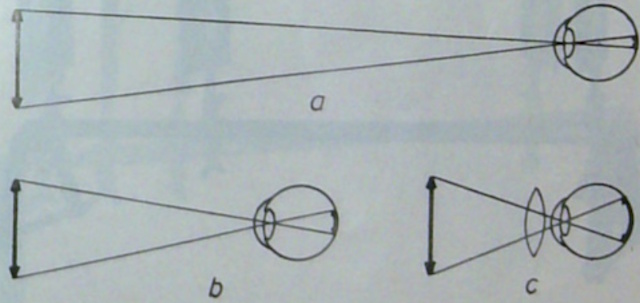
Bij het kijken naar een voorwerp is de grootte van het beeld, zoals dit door het netvlies in het oog wordt weergegeven, afhankelijk van de hoek tussen de lijnen, die van het middelpunt van de pupil tot de uiterste punten van het oog worden getrokken (a).  De gezichtshoek moet niet te klein zijn. Indien de hoek onder een bepaalde waarde komt, kan een normaal oog de details van het voorwerp niet meer onderscheiden. Om een voorwerp zorgvuldig te kunnen bestuderen is het noodzakelijk het zo dicht mogelijk te benaderen zodat de gezichtshoek groot is. Figuur a en b laten zien hoe de gezichtshoek varieert met de afstand t.o.v. het voorwerp. Zonder het oog in te spannen kan de afstand niet worden verkleind tot onder de 25 cm.
Om het voorwerp nog dichter te benaderen, wordt een convexe (bolle) lens voor het oog geplaatst. De gezichthoek kan zo verdubbeld worden (Fig. c) en men zegt dan dat de lens 2 maal vergroot. Een positieve lens die wordt gebruikt om een voorwerp te vergroten wordt een vergrootglas of loupe genoemd.
De benaderende waarde van de vergroting wordt verkregen door 25 te delen door de brandpuntsafstand in cm. De +5, +10 en +15 lenzen kan men gebruiken als vergrootglas.
   
Telescoop of verrekijker
Met een telescoop of verrekijker proberen we gezichtshoek t.o.v. een voorwerp dat men niet kan bereiken te vergroten.
Plaats de +30 lens op 15. Bevestig een frame met witte matglasplaat op 45. Richt het apparaat op een verwijderd en goed belicht voorwerp en stel de lens zo in dat het beeld op het glas scherp wordt.

In dit geval heb ik de hele opstelling op de rug van mijn bureaustoel te leggen  en te richten op een dakkapel ca. 50 m van mij  vandaan.

Het beeld is omgekeerd. Plaats een +10 lens op 55 zodat we het beeld, vergroot met een vergrootglas kunnen bekijken. De korrelige structuur van het matglas zorgt voor een onduidelijk beeld.

Verwijder de witte matglasplaat. Het beeld is nog zichtbaar en duidelijk scherper, als we het door de vergrootglas bekijken. Met dit systeem hebben we een model gemaakt dat men ook wel Keppler's telescoop noemt. De lens van +30 is het objectief van de telescoop.

Projectie op matglas
Opstelling
Projectie op matglas bekeken door lens
 Zonder matglas bekeken door lens
In de aardse verrekijker kan het beeld rechtopstaand verkregen worden door een convexe lens. Plaats de +30 lens zo links als mogelijk is. Plaats de +5 lens op 38cm en de +10 lens op het rechter einde.
 

Opstelling:

 Dat werkt inderdaad zoals beschreven maar het lukte me niet om de telescoop stabiel genoeg te houden om een goede foto te maken.
Een andere wijze van constructie om een rechtopstaand beeld te krijgen is de Hollandse verrekijker. Plaats de +30 lens op 40 cm en de -15 lens op 55. Als men door de concave lens kijkt

 
Een concave lens kan ook als objectief worden gebruikt. Bevestig de concaaf convexe spiegel op 0 en zet deze schuin. Plaats de +10 lens op 30. Het licht dat op het  concave oppervlak van de spiegel valt wordt gereflecteerd. De spiegel produceert ergens tussen spiegel en lens een beeld van het voorwerp. Het is een reëel beeld en kan op een papieren scherm worden opgevangen.  Kijk naar het beeld m.b.v. +10 lens als vergrootglas. Het kan zijn dat de lens verschoven moet worden om een scherp beeld te krijgen. Het beeld is omgekeerd. Het is me niet gelukt om een goed beeld te verkrijgen en zo een goede foto te maken.
   
Microscoop  

Een microscoop bestaat, net als de telescoop, in de meest eenvoudige vorm uit twee convexe lenzen (objectief en oculair). Een microscoop gebruiken we om een zeer sterk vergroot beeld van een klein voorwerp te verkrijgen. Het voorwerp wordt voor het objectief geplaatst op een afstand die enigszins groter is dan de brandpuntsafstand. De brandpuntsafstand van een microscoopobjectief is zeer klein. Het objectief geeft een werkelijk en vergroot beeld van het voorwerp. Dit beeld bekijkt men dan met een vergrootglas, het oculair.

Schroef de +5 lens op 13 cm en de +10 lens op 50 cm. Plaats het object (de dia) in het frame op 6. Stel de lens van +5 (objectief) zo in dat men een scherp beeld door de +10 (oculair) lens kan zien, Plaats om het voorwerp beter te zien de concaaf-convexe spiegel op 0 en draai deze zo dat licht uit een lamp op het voorwerp valt
   
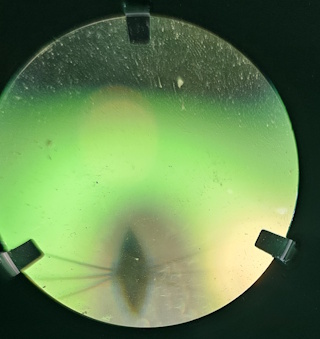Experiment 9: Kleurschifting van het licht

Spectrum
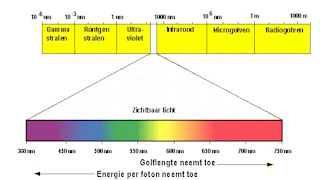
Licht is samengesteld uit verschillende kleuren. Plaats de lamp op 0, met deze zoveel als mogelijk teruggetrokken in de buis. Bevestig de +5 lens op 6 cm en de +12 lens op 9 cm. Plaats het schild met een verticale spleet op 12 cm. Plaats de +15 lens op 31 en de tafel op 34. Zet het prisma op de tafel. Draai het prisma zo dat een spectrum zichtbaar wordt op een geplaatst scherm.
Aan de ene zijde is de strook rood, aan de andere kant violet. Daartussen bevinden zich oranje, geel, groen en blauw. Tesamen vormen deze spectrale kleuren  het spectrum van zichtbaar licht.

Houd een rood glas voor de lens van +15. Alleen het rode licht passeert nu door het prisma en het spectrum bestaat nu alleen uit deze kleur. Herhaal dit  experiment ook met een blauw filter. Men ziet nu geel oranje verdwijnen.
   
Samengestelde en complementaire kleuren
De absorptie van licht verklaart waarom voorwerpen om ons heen gekleurd lijken. Als wit licht een voorwerp bereikt, worden bepaalde kleuren geabsorbeerd, ander gereflecteerd. Dit gereflecteerde en gekleurde licht ontmoet het oog en geeft de voorwerpen hun kleur. Een rood voorwerp reflecteert vnl. rood licht, een blauw voorwerp blauw licht, etc. Een wit papier reflecteert alle mogelijke kleuren waardoor het wit lijkt. Een zwart voorwerp reflecteert helemaal geen zichtbaar licht. Indien objecten door gekleurd i.p.v. wit licht worden belicht wordt een andere toestand geschapen. Indien licht van verschillende kleuren wordt vermengd ontstaat meestal een samengestelde kleur. Onder bepaalde omstandigheden kan wit licht worden verkregen door het mengen van twee kleuren. Men spreekt dan van complementaire kleuren (geel en blauw,  rood en groen, etc.)

Bevestig de lamp op 0, de +10 lens op 10 cm en het frame op 13 cm.  Plaats de beide gekleurde glazen in het frame met de randen tegen elkaar zodat de opening half door het blauwe en half door het gele glas bedekt is. Plaats het scherm op 55 cm. Op het scherm kan men nu een rond belicht vlak zien, waarvan de ene helft blauw is en de ander helft geel. Duw eventueel de lamp wat verder naar voren in de buis. Neem de vlakke spiegel en houd deze verticaal tussen het frame en het scherm en bijna evenwijdig aan de straal. Draai de spiegel zo dat een deel van het gele licht in het blauwe licht wordt gereflecteerd. Waar het gele licht het blauwe  bedekt is het resultaat meestal een witte vlek. Blauw en licht vormen samen wit licht, het zijn complementaire kleuren. Zij moeten echter in de juiste verhoudingen staan.

In werkelijkheid zien we de vlek geel licht die we op het blauwe deel projecteren wat vervagen, "ietwat witter worden".  Geheel wit wordt het echter niet.

   
De diffusie van licht
De ondergaande zon heeft een rode kleur. Als de zon hoog aan de hemel staat vallen de zonnestralen onder bijna rechte hoeken op de aarde en de afstand, die ze door de atmosfeer is zeer kort. Er zijn altijd veel stofdeeltjes in de lucht. Indien wit licht zulke deeltjes ontmoet, verdwijnen de blauwe lichtstralen en treden de rode naar voren. Door de korte afstand door de atmosfeer is het aantal stofdeeltjes niet voldoende om een verandering van belang in de kleur van het zonlicht te brengen. Dat veranderd als de zon gaat dalen. Dan moeten de zonnestralen een aanzienlijk langere afstand door de atmosfeer afleggen en de diffusie van blauw licht wordt groter. Het resultaat is dat de zonnestralen bij het bereiken van de aarde rood zijn.

Plaats de lamp op 0 cm en de +5 lens op 6 cm. Bevestig de +10 lens op 9 cm en het frame met een schild met ronde opening van 2 cm op 12 cm. Plaats de tafel op 16 cm en de +15 lens op 30 cm. Beweeg de lens zo dat een beeld van de ronde opening op de muur verschijnt (ca. 2 m afstand).

Stel de lampin de huls zo in dat de belichting zo gelijkmatig mogelijk is. Deze ronde vlek vertegenwoordigt de zon. 

Om stofdeeltjes in de atmosfeer te simuleren moeten we stofdeeltje smaken.

In fijne poedervorm wordt zwavel neergeslagen uit een oplossing van natriumthiosulfaat indien men daar verdund zwavelzuur aan toe voegt. Los een theelepel natriumthiosulfaat op in 250 ml water. Maak een verdunde zwavelzuur oplossing door wat gec. zwavelzuur toe te voegen aan 250 ml water.

Plaats het plexiglas vaatje op de tafel en giet gelijke hoeveelheden van beide oplossingen in het vaatje. Na enige ogenblikken kan men zien dat de zon geelachtig is geworden terwijl de vloeistof in de pot blauw glanst. Steeds meer zwavel slaat neer in het vaatjes. De zon wordt donkerrood en verdwijnt uiteindelijk volledig.
   

Discussie

Een dergelijke serie experimenten met een degelijke optische bank uitvoeren stond al zeer lang op mijn verlanglijst. Ik heb veel plezier gehad aan het uitvoeren van de experimenten die in de handleiding beschreven stonden maar was ook vaak gefrustreerd. Het is soms ontzettend lastig om het gewenste beeld te verkrijgen en nog lastiger om een scherp beeld te krijgen. Vandaar dat ik soms teruggegrepen heb op wat modernere hulpmiddelen.

Opmerkingen

  • De lux (symbool lx) (van Latijn: licht) is een eenheid van verlichtingssterkte: 1 lux is de verlichtingssterkte voortgebracht door een lichtbron met een lichtsterkte  van 1 candela op een oppervlak loodrecht op de lichtstralen op een afstand van 1 meter van de bron.
  • Resultaten in Excelsheets:
    Resultaten.xlxs

Literatuur:

  • L. Basford, J. Pick; De Lichtstralen - Grondslagen der Optica; De Nationale Uitgeverij; 1966.
  • J.W.G. Wenke; "Beknopte inleiding in de optica"; Centrex; 1966.
  • J.C. Alders; "Ons acoustisch en optisch laboratorium"; Enum; 1948.
  • F.A. Jenkins, H.E. White; "Fundamentals of optics"; 4th Ed; 1976 (1937); ISBN 0070323305.
  • I. Walmsley; "Light - A Very Short Introduction"; Oxford; 2015; ISBN 9780199682690.
  • B. Valeur; "Licht en Geluid - Samenspel van twee natuurkundige fenomenen"; Veen; 2012; ISBN 9789085711223.
  • R.J. Flink; Fysische Optica; Nijgh & Van Ditmar; 1ste druk; 1992; ISBN 9023606728.
  • J.Moors, W. van den Munckhof; 'Licht als golfverschijnsel'; Malmberg; 1ste druk; 1983; ISBN 9020850032.
Relevante websites:

Minder relevante websites:
 

Achtergrondinformatie:
 
De Coachlab lichtsensor 0513BT meet de lichtintensiteit. De intensiteit wordt gemeten in W/m2. De uitgangsspanning van de sensor is evenredig met de lichtintensiteit. Het meetbereik van de sensor is 0,1 W/m2 tot 10 W/m2. De sensor is richtingsafhankelijk. De sensor is gevoelig voor zichtbaar licht en infrarood waardoor deze gebruikt kan worden voor het meten van IR-diodes en zichtbare lichtbronnen.

   
  

28/12/2025