Dendriet kristallen

Datum: Maart 2008 - Maart 2009

Inleiding:

Op 30 maart 2008 heb ik het Geologisch Evenement in Amsterdam bezocht en kwam daar een zogenaamd dendriet kristal structuur tegen. Ik moest onmiddellijk denken aan een elektrodepositie experiment dat ik in het verleden heb uitgevoerd waarbij soortgelijke structuren ontstaan. Ook vond ik een tijdschrift van de Stichting Geologische Activiteiten dat dit onderwerp uitgebreid behandelde. Het leek me leuk om hier iets meer in te verdiepen.

Materiaal:

  • Dendriet
  • Fototoestel
  • Lineaaltje
  • PenScope
  • Computer
  • Software programma: ImageJ
  • Software programma: Python
  • Foto bewerkings Software

Uitvoering:

Naked Eye Inspection (NEI) en Penscope:
  • Maak een foto van het materiaal met een liniaaltje ernaast.
    Op deze manier kan je zien over welke dimensies het gaat.
  • Gebruik de PenScope om meer gedetailleerde opnames te maken (50x, 200x).
Fractale dimensie bepalen mbv ImageJ:
  • Laad de foto in ImageJ.
  • Selecteer het Menu Item "Process" en vervolgens "Make Binary".
  • Save de foto als een raw file
  • Selecteer het Menu Item "Analyze", "Tools" en vervolgens "Fractal Box Count".
  • Klik op "OK" bij het "Fractal Box Counter" scherm.
  • Save en/of noteer de resultaten.

Simuleren mbv de programmeertalen Python en Visual Basic:
Het is mogelijk om fractale patronen te maken door ze te laten tekenen op een computer. In de tijd dat veel computers nog onder MS-DOS draaiden had men daar een programmeertaal, GWBASIC of QUICKBASIC,  voor beschikbaar. Indertijd kwamen veel boeken uit over chaos theorie waarin dan listings van programma's stonden in die talen. In een van die boeken die ik nog in mijn bezit heb, het boek van Lauwerier, stonden voorbeelden van programma's om dit soort patronen te tekenen. Tegenwoordig kan men gratis Microsoft Visual Basic downloaden, hetgeen ook voor dit doel gebruikt kan worden. Ik zocht echter ook naar een mogelijkheid om mijn Acer Aspire One voor dit doel te gebruiken. Deze draait echter onder Linux draait en daar is Basic niet echt een veel voorkomend programmeertaal. Na wat onderzoek kwam ik tot de conclusie dat Python een zeer geschikte programmeertaal was waarin deze Basic programma's in overgezet konden worden. De taal is erg Basic achtig en men kan van een graphics module gebruik maken die erg lijkt op die van QuickBasic. Python is ook standaard binnen Linux aanwezig, men hoeft dus geen ruimte op te offeren (hetgeen ik voor een Netbook wel belangrijk vindt). Python is ook beschikbaar binnen een Windows omgeving. Een van de programma's uit het boek van Lauwerier heb ik vervolgens overgezet naar Python.
Met het resultaat van die simulatie was ik echter niet helemaal tevreden en heb daarom besloten een iets realistischer simulatie te bouwen in Visual Basic.

Resultaat:

NEI en Penscope:

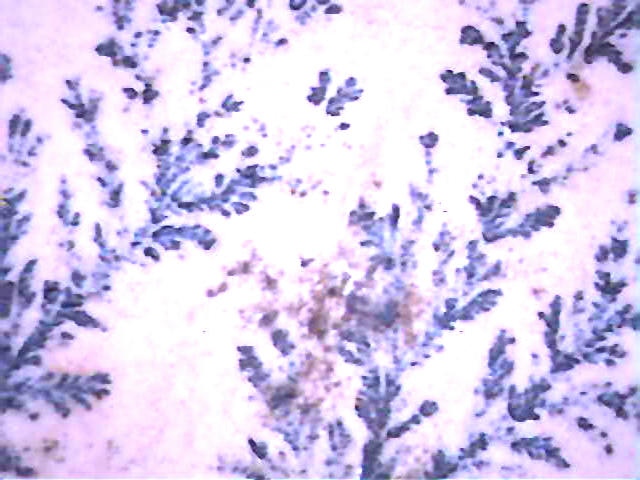
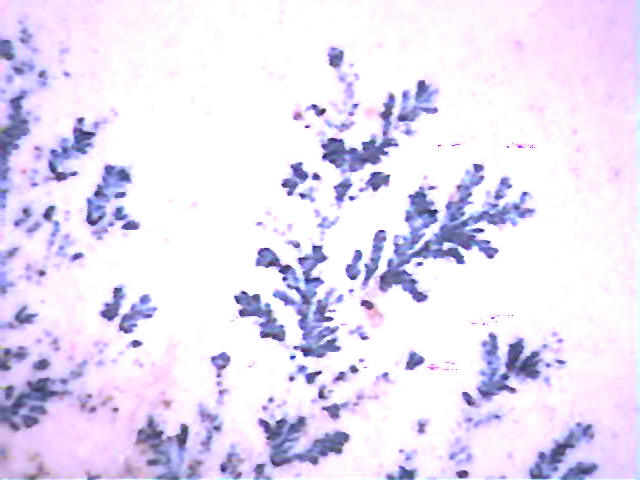
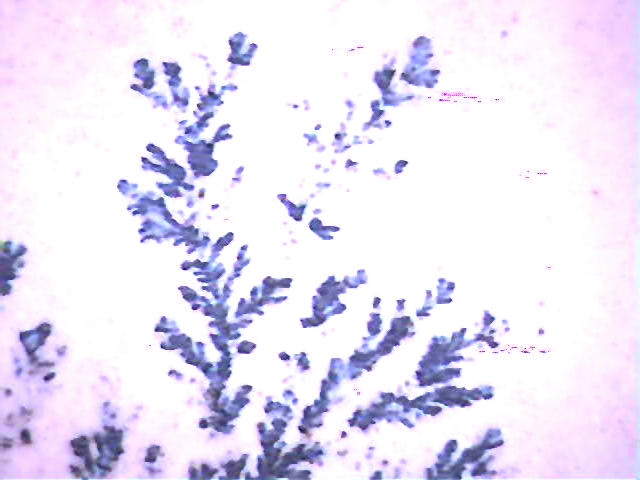
Onderstaande details zijn 50x vergroot mbv de PenScope digitale microscoop.
  Bovenstaande foto is een resultaat van mijn koper-elektrodepositie experiment. 
Alhoewel er duidelijk verschillen zijn is de overeenkomst in struktuur ook erg groot.
In dit geval gaat het duidelijk om een mangaan-dendriet.
Tijdens de vrieskou in januari 2009 viel het mij op dat op de ruit van het schuurtje ijskristallen soortgelijke patronen vormden zoals op nevenstaande foto te zien is.
 

ImageJ analyse:
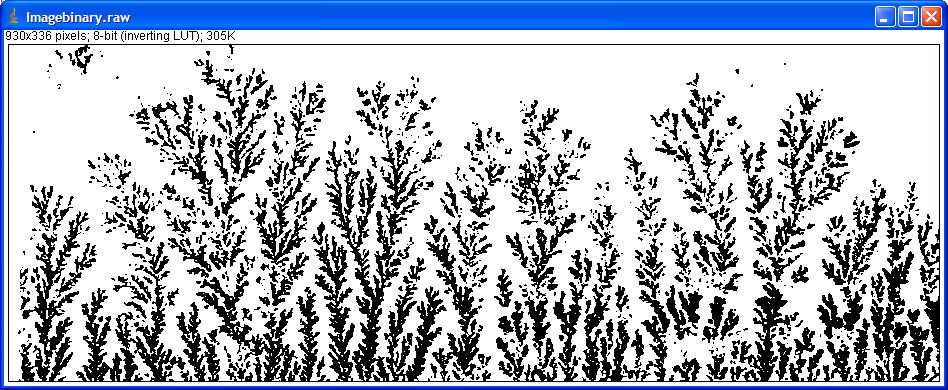
De naar een zwart wit (binair) geconverteerde afbeelding.
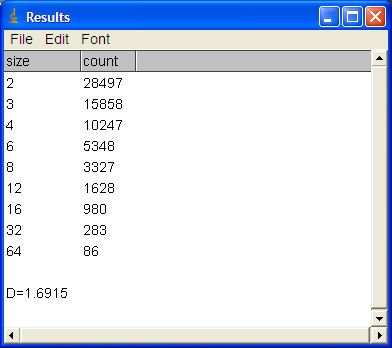
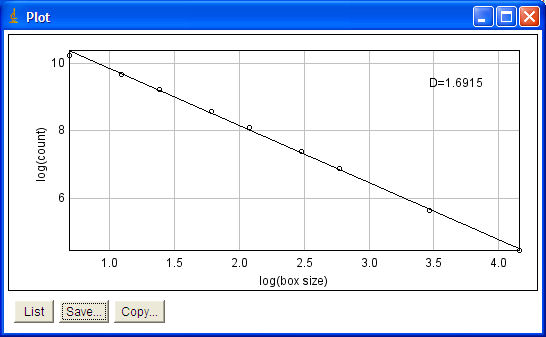
De analyse volgens de box count methode:


Simulaties:
 Een van de programma's uit het boek van Lauwerier heb ik vervolgens overgezet naar Python.
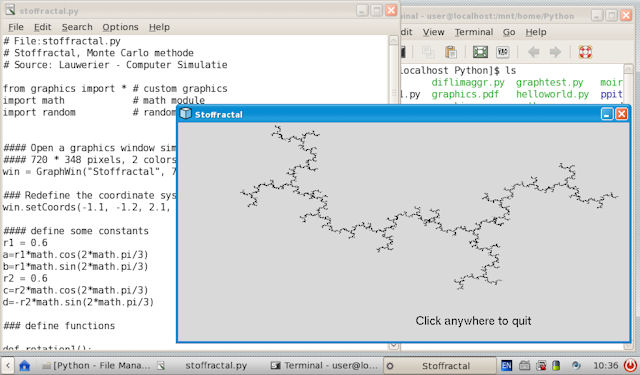
Het resultaat is weergegeven in onderstaand screenshot.
De bijbehorende python code van stoffractal.py:


# File:stoffractal.py
# Stoffractal, Monte Carlo methode
# Source: Lauwerier - Computer Simulatie 

from graphics import * # custom graphics
import math            # math module
import random          # random numbers 

#### Open a graphics window similar to SCREEN 3 in BASIC
#### 720 * 348 pixels, 2 colors
win = GraphWin("Stoffractal", 720, 348)

### Redefine the coordinate system
win.setCoords(-1.1, -1.2, 2.1, 1.2)

#### define some constants
r1 = 0.6
a=r1*math.cos(2*math.pi/3)
b=r1*math.sin(2*math.pi/3)
r2 = 0.6
c=r2*math.cos(2*math.pi/3)
d=-r2*math.sin(2*math.pi/3)

### define functions
def rotation1():
    global x,y,a,b
    z=x
    x=a*x-b*y
    y=b*z+a*y
    return x,y

def rotation2():
    global x,y,a,c,d
    z=x
    x=c*x-d*y+1-c
    y=d*z+a*y-d
    return x,y

def spiegeling1():
    global x,y,a,b
    z=x
    x=a*x+b*y
    y=b*z-a*y
    return x,y

def spiegeling2():
    global x,y,a,c,d
    z=x
   x=c*x+d*y+1-c
    y=d*z-a*y-d
    return x,y

### starting point
x=a
y=b

### picture building
k = 1
for k in range(10000):

  j = random.random()
  if j < 0.5:
   # rotation1()
   spiegeling1()
  else:
   rotation2()
   # spiegeling2()

  #### Draw a point object
  win.plot(x,y)

  k = k + 1

#### Wait for a signal before exiting
message = Text(Point (1,-1), "Click anywhere to quit")
message.draw(win)
win.getMouse()

Bovenstaand programma kan men door een eenvoudige aanpassingen met spiegelingen, rotaties of een combinatie daarvan de fractals genereren.
 
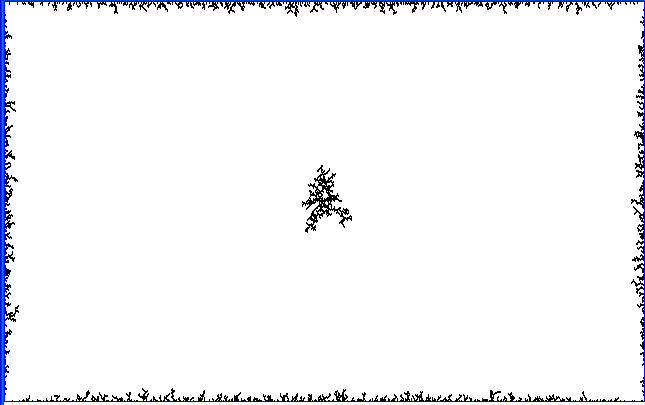
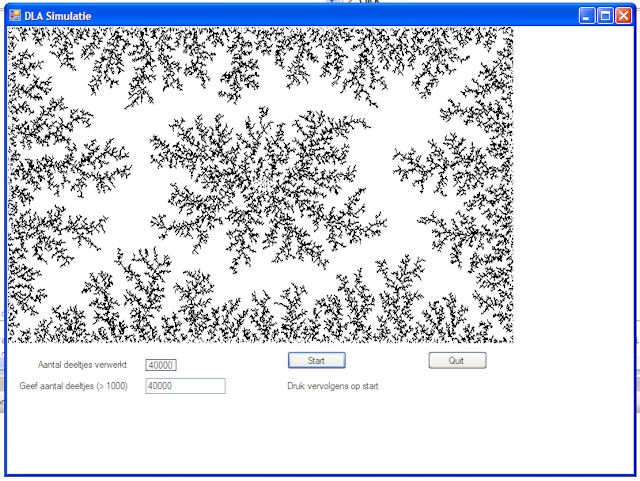
De resultaten van de simulatie m.b.v. Visual Basic zijn weergegeven in onderstaande screenshots die verschillende simulaties op verschillende tijdstippen weergeven. In deze simulatie hebben we een ander principe toegepast dan in het python programma. In het midden van het scherm is een "seed" crystal (pixel) neergezet dat als aggregaat start dient en het is ook mogelijk om op de wanden van de rechthoek aggregaten te laten groeien. Vervolgens plaatsen we op een willekeurige positie in het scherm een kristal (pixel) en laten die willekeurig voortbewegen op een manier die overeenkomt met een Browniaanse beweging. Zodra dit kristal een aggregaat (of wand of seed kristal) tegenkomt plakt het eraan vast. De DLA cluster groeit door de agglomeratie van de diffunderende Browniaanse deeltjes.
De VB code is langer dan de Python code en kan men terugvinden onder achtergrondinformatie.

Discussie:

De meeste dendrieten, zoals hierboven getoond, die in de natuur voorkomen zijn maangaanoxides alhoewel er ook zijn gebaseerd op ijzerhydroxide, silicalitische mineralen, etc. Zoals het elektrodepositie experiment eigenlijk al demonstreert kunnen ook kristallen dendritische structuren vormen (denk bv aan sneeuwkristallen). In dat geval wordt de vorm echter bepaald door de kristalbouw. De vorm van de hier getoonde structuur wordt echter niet bepaald door de kristalbouw.
De dendrieten zoals ze hierboven zijn afgebeeld komen voornamelijk in twee soorten voort de mangaanoxyde dendrieten (Mn-dendrieten) en de ijzerhydroxide dendrieten (Fe-dendrieten) die weer vnl. opgebouwd zijn uit goethiet (FeO(OH)). De Mn-dendrieten zijn gewoonlijk pekzwart terwijl de Fe-dendrieten allerlei schakeringen van bruin, oranje en geel. De takken van de Fe-dendrieten zijn meestal ook breder en grover van structuur dan de Mn-dendrieten, bovendien zijn ze langs de buitenzijde van de takjes meestal sterker gekleurd dan binnenin. De dendrieten hebben een vnl. amorfe structuur hetgeen, zoals hierboven vermeld, ondersteund dat de vorm niet bepaald wordt door de kristalstructuur van de moleculen. De hoek die de aftakkingje maken ligt tussen de 30° en 70°, en meestal zelfs tussen 35° en 55°.
Men heeft verschillende managaanoxide en hydroxide mineralen geïdentificeerd die betrokken zijn bij de dendrietvorming. Enkele van deze mineralen zijn:
  • birnessiet (Na4Mn14O27·9H2O)
  • coronadiet(PBMn8O16)
  • cryptomelaan (KMn8O16)
  • hollandiet (BaMn8O16)
  • romanechiet ((Ba,H2O)Mn5O10)
  • todorokiee ((Ba,Mn,Mg,Ca,K,Na)2Mn3O12·3H2O)
Mn-dendrieten worden op veel plaatsen gevonden maar vnl in kalkgesteentes en dolomieten. Fe-dendrieten komen minde vaak voor en lijken beperkt te zijn tot kalkgesteentes en dolomitische gesteentes. Erg bevorderlijk voor de vorming van de dendrietstrukturen is de aanwezigheid van laagvlakken (scheidingsvlakken tussen twee opeenvolgend lagen).  

  Dendrietvorming op een laagvlak
Een voorwaarde voor de dendrietvorming lijkt te zijn dat de barstdiameter niet te groot is. Het binnendringen van de mangaan- en ijzerverbindingen niet zozeer het gevolg van het oplossen van kalk als wel het gevolg van precipitatie in de poriën tussen de calcietkristallen van het gesteente.   
Deze poriën zijn slechts enkele µm breed. Door de sterke kleuring van het mangaanoxide en door de doorzichtigheid van de kleine calcietkristallen lijkt het of de dendrieten mineralogisch zuivere precipitaten zijn maar in werkelijkheid zijn het dus vertakte stelsels van door Mn- en Fe-verbindingen gecementeerde kalk. Doordat de binnendringing van het discontinuïteitsvlak uit in beide richtingen plaatsvindt resulteert vaneensplijting van lagen in dendrietvormen die nauwkeurig elkaars spiegelbeeld zijn. 

Het meest verbreide type laagvlakdendriet heeft een boomvorm, waarbij een duidelijke hoofdgroeirichting ontwikkeld is. De boompjes beginnen in de meeste gevallen op de "randen" van laagvlakken waar deze door diaklezen doorsneden worden. Van de barsten uit groeien de boompjesdendrieten naar beide kanten, waarbij de hoofdgroeirichting steeds ongeveer loodrecht op de barst staat.
De groei van de laagvlakdendrieten vindt plaats door stoftoevoer die niet (direct) uit de diaklazen komt maar (overwegend) uit de tegenovergestelde richtingen. Het proces speelt zich af in twee fasen:
a. het binnendringen van een oplossing tussen op elkaar liggende lagen, tot op een zekere afstand van de diaklazen, en
b. het afzetten van dit materiaal, eerst op kiemen op de randen van de laagvlakken en vervolgens op de aangroeiende uiteinden van de dendriettakjes.
Met dit mechanisme kan men verklaren waarom de dendrieten een constante takdikte vertonen (de afzettingsduur is overal ongeveer even lang), maar ook waarom de afsplitsingshoeken nooit meer dan 70° bedragen, en de groei naar voren gericht is: groei in achterwaartse richtingen is (in normale gevallen) niet mogelijk omdat de moederoplossing al uitgeput is. 
 
Tegenwoordig zijn er modellen ontwikkeld waarmee de vorm van de dendrieten beschreven wordt. Deze dendrieten zijn random fractals en kunnen beschreven worden met diffusie gelimiteerde aggregatie modellen (DLA). DLA is een proces waarbij deeltjes een "random walk" ondergaan die wordt bepaald door de Browniaanse beweging, vervolgens samensmelten en zo aggregaten van dit soort deeltjes vormen. De theorie is toepasbaar op vele systemen waar diffusie het primaire transport mechanisme vormt. DLA kan men waarnemen is systemen zoals elektrodepositie, Hele-Shaw flow patronen en, zoals in dit geval, minerale afzettingen.
 
We kunnen de fractale dimensie van deze dendrieten bepalen m.b.v. software die foor dit doel ontwikkeld is. In dit geval hebben we gebruik gemaakt van het programma ImageJ. Hiermee hebben we een waarde van D=1.69 gevonden. De vraag is dan nu hoe betrouwbaar dit resultaat is en om dat te kunnen beoordelen moeten we het vergelijken met de waardes zoals we die in de literatuur kunnen vinden.

In de literatuur kunnen we waardes voor dendrieten vinden:

  • Sander in Scientific American
    D=1.71 voor een Zn metaal depositie
    D=1.71 voor het computer gegenereerde fractal patroon.
  • Bayirli et al in Physica A
    D=1.659-1.822 voor Mn dendrieten
    D = 1.657 voor DLA
  • Chopard et al in Nature
    D=1.51 - 1.79
    D~1.70 voor DLA simulaties
  • Merdan et al in Chin.Phys.Lett.
    D~1.61-1.88  voor Mn dendrieten.

De door onze gevonden waarde past dus perfect in de range die voor dit soort Dendrieten in de literatuur gegeven wordt.
 
Betreffende de Python simulatie die gedaan is het noodzakelijk dat men zich realiseert dat alhoewel men met de code zoals we uit het boek van Lauwerier gehaald hebben een figuur maken die lijkt op de figuren zoals we ze in de natuur waarnemen we hier niet hetzelfde patroon creëren als we in het gesteente waargenomen hebben. In het model dat we hier simuleren gaan we uit van een puntbron die zich in alle richtingen kan verspreiden. Het is echter geen simulatie van het proces zoals dat plaatsvindt in de natuur waarbij een dendriet vorm gecreëerd wordt oftewel het DLA proces wordt niet echt gesimuleerd met deze programmacode. In het gesteente zien we geen startpunt maar iets wat meer op een startlijn lijkt. We passen als het ware alleen maar een wiskundig truckje toe, we simuleren niet echt zaken zoals chemische reacties en transportverschijnselen.
Dat bezwaar hebben we proberen te ondervangen m.b.v. de simulatie die we in VB hebben geschreven. Deze is ook realistischer in het nabootsen van het proces zoals het werkelijk plaatsvindt. Desalniettemin is het niet een perfecte match. Het is interessant om te zien dat groei vanaf de wanden vnl in het midden plaatsvindt. Dit is verklaarbaar als men zich realiseert dat als er eenmaal wat aangroei heeft plaatsgevonden de kans groter is dat een zich willekeurig voortbewegend deeltje in het midden een aangroeipunt vindt voordat het in de hoekpunten is aangekomen.

Conclusies:

  • M.b.v. de boxcount methode is een fractale dimensie van D=1.69 voor de de bestudeerde dendriet gemeten.

Literatuur:

  • L M J U van Straaten; 'Dendrieten'; GEA; 21 2 1988;  p. 37-46.
  • Andrew Harrison; 'Fractals in Chemistry'; Oxford University Press; 1995; ISBN 0198557671; p. 39,40.
  • B. Chopard, H.J. Herrmann, T. Vicsek; "Structure and growth mechanism of mineral dendrites"; Nature; 353 1991; p. 409-412.
  • Z. Merdan, M. Bayirli; "Computation of the Fractal Pattern in Manganese Dendrites"; Chinese Physics Letters; 22 8 2005; p. 2112-2115.
  • M. Bayirli; ''The geometrical approach of the manganitise compound on the surface of manganasite ore"; Physica A; 353 2005; p. 1-8.
  • Hans Lauwerier; 'Fractals'; Aramith; 1987; ISBN 906834031X.
  • Leonard M. Sander; "Fractal growth processes"; Nature; 322 28 August 1986; p. 789-793.
  • Larry S. Liebovitch and Tibor Toth; "A Fast algorithm to determine fractal dimensions by box counting"; Physics Letters A; 141 8,9 1989; p. 386-390.
  • Cathal G. Dillon, Paul F. Carey, Richard H. Worden; "Fractscript: A macro for calculating the fractal dimension of object perimeters in images of multiple objects"; Computers & Geosciences; 27 2001; p. 787-794.
  • Leonard M. Sander; "Fractal Growth"; Scientific American; January 1987; p. 82-88.
  • Paul S. Addison; 'Fractals and Chaos - An Illustrated Course'; Institute of Physics Publishing; 1997; ISBN 0750303999; p. 79,80.

Relevante websites:

Minder relevante websites:

Opmerkingen:

  • Een microscoop is makkelijk maar een goed vergrootglas voldoet natuurlijk ook.
  • Het woord dendriet is afgeleid uit het Grieks: dendron = boom.
  • DLA = diffusion limited aggregation.
  • De python files zijn downloadbaar:
    stoffractal.py
  • De VB code is downloadbaar als rar file: DLA Simulatie.rar
  • In dit experiment heb ik voor Python en Visual Basic gekozen als programmeertalen. Men kan natuurlijk ook voor andere programmeertalen kiezen.
  • Voor het maken van deze grafieken mbv Python heeft men een graphics module nodig: graphics.py. Die men in dezelfde map als waarin het programma staat geplaatst wordt. Deze kan men downloaden van: http://mcsp.wartburg.edu/zelle/python/

Achtergrondinformatie:

Wat is een fractal?

Een fractal is een meetkundige figuur waarin eenzelfde motief zich steeds op kleinere schaal herhaalt. Dit patroon kan men in de natuur zeer vaak herkennen. Een goed voorbeeld is een boom met een stam die zich splitst in twee kleinere zijtakken, die zich op hun beurt weer splitsen in twee kleinere zijtakken die zich op hun beurt weer... ad infinitum.

De specifieke kenmerk van gelijkvormigheid die fractals hebben heeft ook als gevolg dat als we maar een klein stukje van een fractal kennen van daaruit de gehele structuur kunnen herleiden. Een ander kenmerk van fractals is dat ze gebroken dimensies hebben. Waar een punt een dimensie 0 heeft, een lijn een dimensie 1, een vierkant een dimensie 2 en een kubus een dimensie 3 hebben fractals dimensies die daartussen liggen. Bij een foto reduceert men een fractal naar een tweedimensionale vorm en voor een fractal geldt dan vaak dat deze een dimensie tussen 0 en 2 krijgt. Het laatste specifieke kenmerk van een fractal is dat deze in principe ontstaat door oneindige iteratie. Uitgaande van een basisfiguur voert men daar een bewerking op uit. Op het resultaat van die bewerking laat men weer dezelfde bewerking los, ad infinitum.

De fractale dimensie kunnen we bepalen m.b.v. de formule van Hausdorff-Besicovitch die luidt:

Hierin is D de dimensie en N(h) het aantal schijven van grootte h dat nodig is om een object te bedekken.

Passen we de formule toe op een lijn dan krijgen we de volgende analyse: 1 schijf van grootte 1, 2 schijven van grootte 0.5, 4 schijven van grootte 0.25 etc. In de limiet vinden we dan een dimensie van:

Passen we deze formule toe op de driehoek van Sierpinsky.

De schaal van de uitvergroting is 2 is en dat de driehoek komt telkens 2 keer voor in de oorspronkelijke driehoek.

2^D = 3
log(2^D) = log(3)
D*log(2) = log(3)
D = log(3)/log(2)
D = 1,585

De driehoek van Sierpinsky heeft dus een fractale dimensie van 1,585.

In de box count methode (vierkantjes tellen) legt men een grid van vierkantjes van verschillende groottes over het plaatje dat het object bevat. Het aantal vierkantjes N(h) dat een deel van de fractal bevatten wordt geteld. De fractale (box) dimensie D wordt gegeven door de hellingshoek van de lijn die men krijgt als men log(N(h)) tegen log(1/h) uitzet.  Aangezien er geen vastgelegde grootte is voor de vierkantjes t.o.v. het aantal pixels in de afbeelding zijn meerdere metingen van N(h) voor verschillende groottes nodig. De grafische waarde van N(h) is meestal een gemiddelde voor verschillende groottes.


Visual Basic 2008 Code:
Public Class frmSimulatie

'Simulation of Diffusion limited aggregation (DLA)

'We start with an immobile seed on the plane.
'A walker is then launched from a random position and
'is allowed to diffuse. If it touches the seed, it is immobilized
'instantly and becomes part of the aggregate. We then launch similar
'walkers one-by-one and each of them stops upon hitting the cluster.
'After launching a few hundred particles, a cluster with intricate
'branch structures results.

Dim counter As Integer 'simulation loop counter

Sub DLASimulation(ByVal frmTst As Form, ByVal counterMax As Integer)
'Prepare grphs variable for graphics calls
Dim grphs As System.Drawing.Graphics

grphs = frmTst.CreateGraphics

Dim ScreenArray(640, 400) As Boolean 'used to keep track of pixels set
Dim x, y As Integer 'form coordinates
Dim MovePixel As Integer '
Dim test As Boolean 'Check on whether a pixel is set
Dim i, j As Short 'counters
'Dim counter As Integer 'simulation loop counter
'Dim counterMax As Integer 'Max number of loops
'Define Pen colors
Dim PenBlack As New System.Drawing.Pen(System.Drawing.Color.Black, 1)
Dim PenRed As New System.Drawing.Pen(System.Drawing.Color.Red, 1)
Dim PenWhite As New System.Drawing.Pen(System.Drawing.Color.White, 1)
Dim PenBlue As New System.Drawing.Pen(System.Drawing.Color.Blue, 1)

'InputBox("Geef aantal seeds (> 1000)", counterMax)
'counterMax = 1000
'Initialize the array by putting all its elements on False
For i = 0 To 640
For j = 0 To 400
ScreenArray(i, j) = False
Next
Next

'-----------------------------------------
'Setting up the screen
'-----------------------------------------

'Draw lines that define the system boundary and set the corresponding Array elements on true
grphs.DrawLine(PenBlue, 0, 0, 640, 0)
For i = 0 To 640
ScreenArray(i, 0) = True
Next
grphs.DrawLine(PenBlue, 640, 0, 640, 400)
For i = 0 To 400
ScreenArray(640, i) = True
Next
grphs.DrawLine(PenBlue, 640, 400, 0, 400)
For i = 0 To 640
ScreenArray(i, 400) = True
Next
grphs.DrawLine(PenBlue, 0, 400, 0, 0)
For i = 0 To 400
ScreenArray(0, i) = True
Next

'---------------------------------------------
'This is were the DLA simulation starts
'--------------------------------------------

'The starting point i.e. the seed we position in the middle
x = 320
y = 200
grphs.DrawEllipse(PenBlack, x, y, 1, 1)
ScreenArray(x, y) = True

i = 0

Do
'Generate a starting point for the walker but make sure it is not a
'a border or somewhere else that is already occupied.
Do
x = Int(Rnd() * 640)
y = Int(Rnd() * 400)
Loop Until (ScreenArray(x, y) = False)

'Let the walker run around until it meets an aggregate, seed or border
Do While test = False
'grphs.DrawEllipse(PenBlack, x, y, 1, 2)
'check whether a point is adjacent to another point
'If (x = 0 Or x = 640) Or (y = 0 Or y = 400) Then Exit Do
test = ScreenArray(x + 1, y) Or ScreenArray(x - 1, y) Or ScreenArray(x + 1, y + 1) Or ScreenArray(x, y + 1) Or ScreenArray(x - 1, y + 1) Or ScreenArray(x + 1, y - 1) Or ScreenArray(x, y - 1) Or ScreenArray(x - 1, y - 1)
If test = True And (ScreenArray(x, y) = False) Then
'I want to stick to the aggregate or to a border
grphs.DrawEllipse(PenBlack, x, y, 1, 1)
ScreenArray(x, y) = True
test = False
Exit Do
Else
'grphs.DrawEllipse(PenWhite, x, y, 1, 1)
'We keep moving around until we meet a aggregate
'Use a Random number to determine where to go to
MovePixel = Int(Rnd() * 8)
'Determine which move to be made
If MovePixel = 0 Then
x = x + 1
ElseIf MovePixel = 1 Then
x = x - 1
ElseIf MovePixel = 2 Then
y = y + 1
ElseIf MovePixel = 3 Then
y = y - 1
ElseIf MovePixel = 4 Then
x = x + 1
y = y + 1
ElseIf MovePixel = 5 Then
x = x + 1
y = y - 1
ElseIf MovePixel = 6 Then
x = x - 1
y = y + 1
ElseIf MovePixel = 7 Then
x = x - 1
y = y - 1
End If
'We assume that once a particle touches a border it is gone
'and we start with a new particle.
If (x = 0 Or x = 640) Or (y = 0 Or y = 400) Then Exit Do
End If

Loop
counter = counter + 1

'ensure that the labels are updated and buttons are accessible
lblCounter.Text = counter
lblCounter.Refresh()
lblCounter.Update()

'ensure that buttons are accessible when the sim is running
Application.DoEvents()

Loop Until counter = counterMax

End Sub

Private Sub btnQuit_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles btnQuit.Click
End
End Sub

Private Sub btnStart_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles btnStart.Click
DLASimulation(Me, Me.txtMaxCounter.Text)
End Sub

End Class

22/12/2009